We are going to describe a particle using a wave function. The evidence of this occurs during electron diffraction. A harmonic wave traveling in the +x direction has the form..
For ease, we want to transform this into the complex plane.
Where k is the wave number and omega is the angular frequency. In general omega will be related to k in some way.
Psi only has one spatial dependence, namely x. Meaning it does not change in y or z and is thus called a plane wave for all possible values of k. We know that the amplitude depends on the frequency, and we know that the frequency depends on the wavelength, AND we know the wavelength depends on the wave number. Thus, we will be writing the amplitudes of the waves as functions of k, because they are inherently a function of wavelength which is inherently a function of frequency. We will not be restricting the amplitudes A(k) to real space. We will see shortly that A(k) at anytime is inherently a complex number.
Light exists as both a particle and a wave. What we will do now is construct a particle using a superposition of an infinite amount of waves. The waves will cancel everywhere except for a small packet, which will make up a particle. The mathematical construct is as such.
We will now assume another condition amongst the waves. We will assume that they are generally around the same wave number k_0, while there will exist some waves that are not around this value, the majority of them will be. A good description of this distribution is the Gaussian Distribution. So we assume this is the function that describes the amplitude and plug that into the integral.
Since the Gaussian distribution doesn't have a finite width, it does however get to a point where the contributions are negligible. We will define this point to be at the point where the exponent reaches -1 in the "e" expression for A(k).
This "width" will be important to us a little later. We will now evaluate the integral.
So we end up with a plane wave factor that depends on the wave number k_0, and a "modulating" factor to localize the packet around x=0 (This factor is Gaussian). We now square the function and set this factors exponent equal to -1 to get the "width" of the wave packet.
The number on the right hand side is of little importance, in general however, this number is always less than 1/2. This is simply a consequence of Fourier integrals. This is known as Heisenberg's uncertainty principle.
How Wave Packets Move:
Recall from optics class that the group velocity of a wave is..
We will now attempt to derive an expression for the motion of the wave packet at any time t. So we again start with the following integral.
In order to evaluate this integral, we need to know how omega depends on k. We start by approximating omega in its Taylor series expansion.The integral is evaluated in much the same way as the previous one.
This equation has no meaning at this point, it is a complex function that describes the position of a particle. What IS useful is the magnitude of this function. The magnitude of this equation is interpreted as the probability of the position of the particle.
This is a real values function as thus useful to use when taking measurements.
Notice the difference between this amplitude and the amplitude of the wave packet at t=0. As time increases, the amplitude actually spreads out due to the t^2 term in the denominator. So you might be thinking, how can this describe a particle? A particle doesn't spread out as it moves. That's correct, but I stated earlier, the magnitude is interpreted as the probability and thus, as time increases the space where the electron is likely to be found increases.
The Schrodinger Equation
We use the following formulas to re-write the wave packet formula. The first being from the de Broglie relation and the second being from the Planck relation.
An interesting thing to note is that the group velocity is..
The above wave equation is for a free particle with no restrictive potential stopping it. But what if we did indeed have a potential?
The first instinct is to simply plug this into our integral and evaluate it. What we will find however is that we get a solution that doesn't change the nature of the motion at all even with the potential! This is incorrect. The best way to go about finding a solution to this problem is first forget about the potential, and construct a partial differential equation that describes the wave function, from here we can insert the potential.
The first thing we do is differentiate with respect to time and multiply by i times h-bar.
We also differentiate with respect to x twice and multiply by another factor. (Just to get rid of the extra i's and h-bars)
This is the Schrodinger equation for a free particle.
The following is a direct excerpt from the book.
"Although we started with the solution to the above equation, the equation takes precedence over the solution. It is easy to see that starting from the solution, a function of e^(kx+wt) would correspond to a negative kinetic energy and that Acos(kx-wt)+Bsin(kx-wt) will only be a solution if B=iA. To the extent that, the above equation is a translation of E=p^2/(2m). With E and p being replaced by operators."
So the Schrodinger equation is a statement of Energy. Namely, the kinetic plus potential energies is equal to the total energy. This can be generalized by adding a potential term.
This is the general Schrodinger Equation.
We will now return to the free particle case. The general equation depends on what Phi(p) is. This is determined by the initial condition, namely Psi(x,0). This is in contrast by the typical wave equation that requires both Psi and its time derivative to be specified. This is because the Schrodinger Equation is only dependent on the first time derivative, not the second as is the case for the normal wave equation.
The equation at t=0 is.
We can see that Psi is just a Fourier transform of Phi. This Phi can be expressed in terms of Psi by inverting the Fourier integral.
Let us jump back real quickly to the Heisenberg Uncertainty Principle, we brought it up when we were discussing wave packets but it works equally well here. We use the relation we had earlier and remember that p=hk thus..
The Probability Current
Since the magnitude of the wave equation represents the probability density of a particles motion, we must require that.
If this is not equal to 1, then we can easily multiply the above integral by a constant A in order to make it 1. The constant A must be a constant in order for the probability integral to be normalized. We now show this. Starting with the Schrodinger equation, we assume the potential is entirely real and first find the complex conjugate.
We now define the flux, or probability current as the term in the brackets. We get...
The last step follows from the fact that square integratable functions are zero at plus and minus infinity. The following is a direct quote from the book.
"Incidentally, had we allowed for discontinuities in Psi(x,t) we would have been led to delta functions in the flux, and hence the probability density, which is unacceptable in a physically observed quantity. Thus the above equation implies that A is constant."
The above equation is a conservation law, analogous to the charge conservation in electromagnetic theory. It states that the change in the density in a region, say a<=x<=b is compensated by a net change in flux into that region.
Expectation Values and the Momentum in Wave Mechanics
Recall from Statistics, the way in which we calculate the expectation value of something. For any function f(x) we have...
This is fine for calculating the expectation value of position, but how would we calculate the expectation value for momentum? What would we put between the two Psi's? We approach this by noting that clasically we have the following relation..
Because the wave functions vanish at infinity (Exactly what happened with the probability current!), the first term does not contribute and the integral gives...
The last step follows again that the wave function is a square integratable function and is zero at plus and minus infinity. The proof uses the logic that since the difference between the complex and real expectation value is zero, they must be the same value, namely real.
Even when the wave function is not square integratable, and a periodic function is used, it still yields the same solution.
An operator whose expectation value for all admissible wave functions is real is called a hermitian operator. Thus the momentum operator is hermitian.
The form of the momentum operator allows us to re-write the Schrodinger Equation.
Where H is the Hamiltonian operator.
The Wave Function in Momentum Space
We have previously found a way to represent momentum. Let us turn our focus back on Phi. We found the form of Phi to be..
Let us calculate the following..
This is known as Parseval's Theorem, which states that if a function is normalized, so is it's Fourier Transform.
Let us do another calculation..These two results strongly suggest that Phi should be interpreted as the wave function in momentum space. This is due to the entirely symmetrical nature it shows compared to what we have calculated in the past for Psi.
We calculated the operator for momentum earlier as a differential expression and the x operator was simply x. In momentum space however, the momentum operator is simply p and the x operator is a differential operator. By using the same exact methods used to derive the momentum operator, one finds that the x operator in momentum space is...

































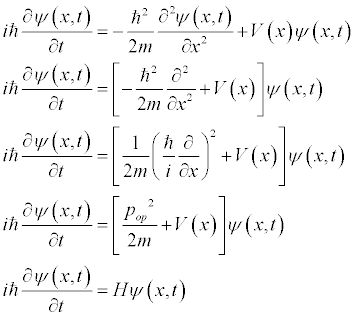




No comments:
Post a Comment