This post will deal with one dimensional potential functions in the Schrodinger equation. The first one we will look at is the Potential Step.
The Potential Step:
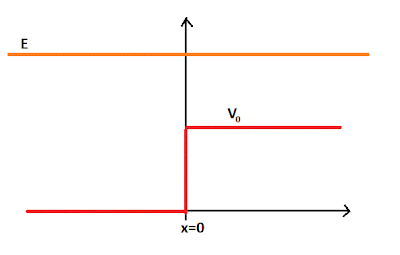
This problem has the following potential function.
We will start with the time independent Schrodinger Equation..
Before x=0 and after, the solution will be different. (Slightly, only by the magnitude of E-V compared to just E.) When x<0 we have..
To see a post that includes what the flux, or probability current is, go here.
We can view e^(ikx) as an incoming wave with probability current (h-bar)k/m. If there was no potential function, then this alone would suffice for the solution to the time independent Schrodinger equation. Therefore we can attribute the second term to the term caused by the potential ie, the reflected wave with flux [(h-bar)kR^2]/m. R is the reflection coefficient.
We now need to investigate the behavior of the wave function after the point x=0.
The second term must be equal to zero because in our "experiment" wave is coming from the minus x direction and this term would only yield zero (at infinity) if it was coming from the +x direction. Thus our solution is..
Where T is the transmission coefficient.
We now calculate the flux or probability current of this solution..
It is important to note that even though the wave function is discontinuous at x=0, the wave function is not. The slope (or rate of change) of the wave function is also continuous. We show this by integrating the time independent Schrodinger equation over a small distance -e to e. (e is epsilon)
Which implies continuity of the wave function's derivative.
We now take the two equation that we have above, and solve for R and T.
We can now use these results to calculate the fluxes.
An interesting thing to note is if E is less than V, then q becomes imaginary, and we get an exponential decay "through" the barrier. It can be shown (not that hard) that R^2 in this case is equal to 1, thus we would have total reflection, however there is still partial "penetration through the barrier" this allows, for a "thin" enough barrier for the wave to "tunnel" through.
The Potential Well:
The next situation we will investigate is the potential well. It has the following potential function.
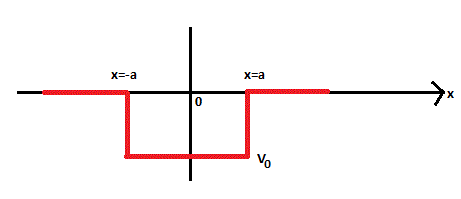
We can immediately write down the solutions based upon the logic from the previous discussion. (Where k and q have the same values as before.)
We now impose the same conditions for continuity. However, we will combine the conditions into one expression that must be true for each solution. Remember, both the wave function and its derivative must be continuous at the discontinuities.
We now use this condition for each discontinuity.
We now solve these two equations to eliminate A and B.
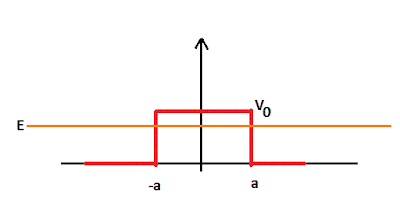
The Potential Barrier:
We now consider a similar situation, the potential barrier. It has the following potential function.
We will examine what happens inside the barrier. We again start with the time independent Schrodinger equation.
We will examine what happens inside the barrier. We again start with the time independent Schrodinger equation.
If (kappa)*a >> 1, then this simplifies to...
This, even though the energy is below the potential barrier, there is indeed transmission through the barrier. This transmission is extremely sensitive to the width of the barrier.
The Harmonic Oscillator:
Now we get to the meat and potatoes of this post. The quantum harmonic oscillator. This problem deals with a spring potential energy function. We will start out with the Hamiltonian for this problem and construct the Schrodinger equation for this situation.
For any eigenvalue of epsilon, as y^2 approaches infinity, the term involving epsilon is negligible, thus we require that u(y) asymptotically follow the equation....
We will now find the homogeneous equation. (We are solving this similar to the variation of parameters approach.)
The way we will solve this is by using a series solution.
When this is inserted into the equation for u(x), we get a solution which does not terminate at infinity. The way to solve this is to have the solution terminate at certain values of epsilon, namely epsilon=2n+1.
For these values of epsilon, the series terminates and the recursion relation yields..
The function h(y) is known as the Hermite Polynomials.

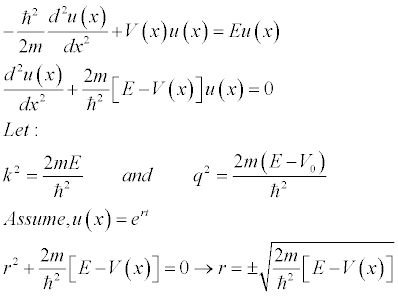
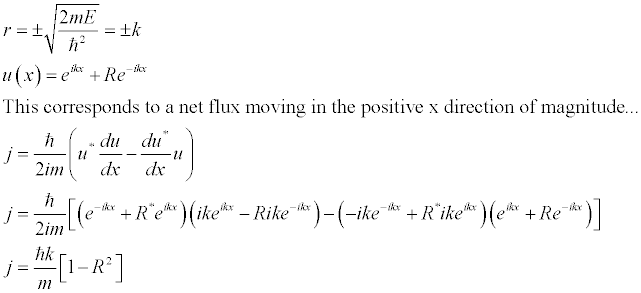
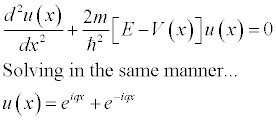


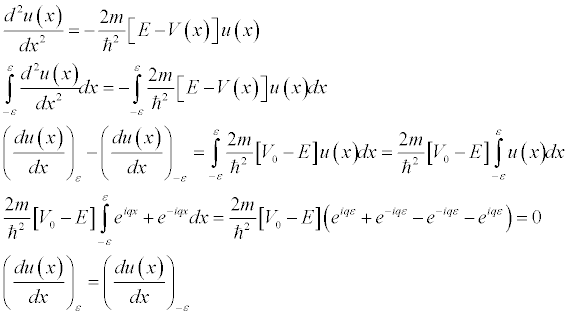
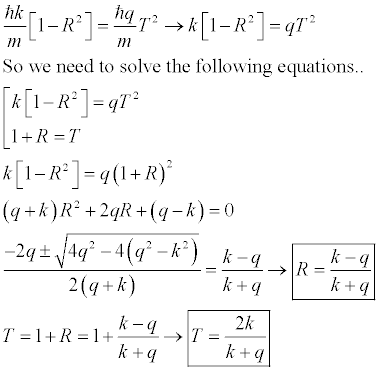



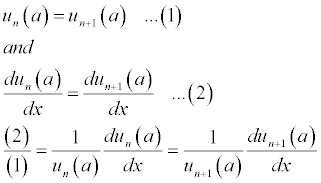


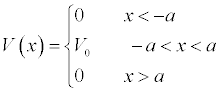





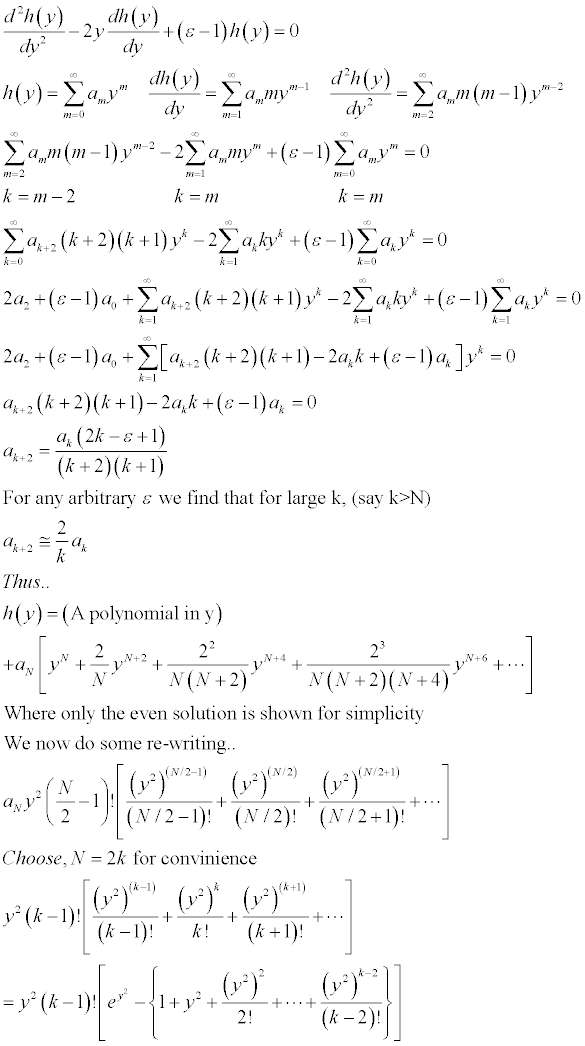

Excuse me could you please show the steps you used to solve the two equations for the potential barrier .I have scartching my head trying to figure out how to find the constants .I can t find it anywhere .Please help this noobie in maths
ReplyDeleteI mean the potential well not potential barrier .
ReplyDelete