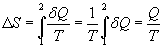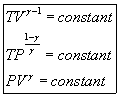Entropy

The first topic of this post will be about the Clausius Inequality.  So Clausius knew that the following relationship held for a reversible engine.

The question is, how does this relationship hold up for irreversible engines?  Well he did some experiments! Obviously for a reversible engine, the two terms on the left hand side are equal to one another, but what happens in an irreversible engine?  As you can imagine, there are many irreversibilities in an irreversible engine, friction being one major example.  These irreversibilities consequently cause the work output of the engine to be less, and cause the heat output of the engine to be more.  Therefore, for an irreversible engine, the second term on the left hand side of the above equation is greater than the same term in a reversible engine.  If we divide a power cycle into an infinite amount of small cycles, and sum the quantity Q/L up for each one we obtain the following relationship. (The integral takes into account heat entering AND leaving.)

This is what is known as the Clausius inequality.  Notice that we indicate that the integral is over a cycle by using a circle over it.  (The circle should be in the middle of the integral, my math type program is weird like that.)  The above expression is an equality when the cycle is reversible and an inequality when the cycle is irreversible.

If we think about what this means, we realize that this expression is acting like a thermodynamic property.  Just as the change in internal energy, volume and other properties of a cycle are equal to zero, so is this expression.  Clausius realized that this represents a new thermodynamic property which he called entropy.  He defined it as such..

To obtain the change in entropy, one would integrate both sides.  Notice that the differential for heat is an inexact differential, this is because heat is a path function, not a state function!  Also realize that we define entropy as the change in entropy not what entropy is specifically.

So what does this mysterious property tell us?  Entropy is very abstract and requires a bit of thought to first understand.  When it boils down to it, entropy is a direct measure of disorder.  The definition of entropy is part of the second law of thermodynamics, which basically says that energy has quality as well as quantity, and when energy is used in a device with irreversibilities, some of that energy gets dissipated into a less useful, more disordered form, heat essentially.  If we go back to the engine in the beginning of this post, the second term turned out to be larger than the first because of the internal irreversibilities.  This means that there was more entropy at the end of the cycle than at the beginning because the difference of the two entropies is negative.  This means that entropy is generated due to irreversibilities.  This is in contrast to energy which can never be created or destroyed.  So because the Clausius inequality is less than or equal to zero, and since we know that it is impossible to have an irreversible process in real life, we can say that all processes generate entropy, and the entropy or disorder of the universe is constantly increasing.

An interesting thing happens when we look at a system that is undergoing an isothermal process. (T=constant)

Imagine that we are undergoing a cycle that has two paths.  The path from point 1 to point 2.  And the path (which is different than the first) from point 2 to point 1.  If the path from 2 to 1 is reversible, and the path from 1 to 2 is either irreversible OR reversible from the Clausius inequality..

So the change in entropy is always greater than or equal to a process that is either irreversible (the inequality holds) or reversible (the equality holds).  If we want to equate these two terms we would need to add another term on the right hand side.

This relationship is valid of any process, reversible or irreversible.  When the process is irreversible, the entropy generated is equal to some value, and when the process is reversible, the entropy generated is equal to zero.  A trick into calculating the entropy generation is to take the system and its surroundings as one big system, therefore the entropy generated would be equal to the change in entropy of the system plus the change in entropy of the surroundings.  (One will be negative, and the absolute value of one of them will be greater than the other because of the entropy generated.)

The reason why entropy defines the second law is because it allows us to determine if the direction of a process is possible.  The first law of thermodynamics does not, it would have no problem saying that a cup of hot coffee would get hotter as it sits on the table in the cold.  This defies the second law however because the second law states that all processes must continue in the direction of increasing entropy.  If the coffee cup were to get hotter, the surroundings would get cooler, which is a decrease in entropy of the surroundings without the addition of work.

If we rearrange the definition of entropy and then plug into the first law..

This is what is known as the combined statements between the first and second law.  If we recall the definition of enthalpy, we can get another expression in terms of enthalpy.

We are going to use these formulas to find out how to calculate the entropy change of solids and liquids, and then ideal gases. For solids and liquids, we will use the first equation and realize that a solid or a liquids change in volume is negligible, therefore PdV is approximately equal to zero.  Remembering that dU=cdT..

If we wish to approximate it, the change in temperature shouldn't be over 100 K or so, otherwise the error becomes larger and larger.  To do this, we will take the average value of the specific heat capacity over the temperature change.

If we undergo an isentropic process, the change in entropy is equal to zero. (Isentropic means, constant entropy.) So then..

Therefore, an isentropic process with an incompressible substance is also isothermal.

So now we move on to ideal gases.  We again use the combined statements of the first and second law.  All we need to do is substitute du=CvdT, and P=RT/V into the first equation and dh=CpdT,V=RT/P into the second equation, and then integrate. (Note: We will again be using the average specific heat capacity approximation.)

Various relations can be derived from these equations in an isentropic process. (The change in entropy is equal to zero.)   If we set the first equation equal to zero..

In a similar manner, we can do the same thing with the other equation.

To get the third relation, we simply combine both of these expressions since they both equal the ratio of the two temperatures.

These three equations can be expressed in a compact form as...

Entropy allows us to construct an entropy balance for a problem.  There is no conservation of entropy but we can still do an entropy balance if we include the entropy generation term.

Let's recap the ways entropy can interact with the system.

Entropy enters or leaves a system through the boundaries.  Therefore in an adiabatic closed system, the entropy change is equal to zero.

1. Heat Transfer:

Heat is is a major factor in entropy gain or loss.    Heat transfer into the system causes the entropy of the system to rise, and on the other hand, heat transfer out of the system causes the system to lose entropy.

2. Mass Flow:

Another way entropy can change in the system is due to mass flow through the boundaries.  If the system is closed then there is no mass flow, and hence no change in entropy due to mass.

3. Entropy Generation:

Remember, all real processes have irreversibilities, hence all processes generate entropy. The only type of process that does not generate entropy is the idealized reversible process.

That about wraps up this post on Entropy!

The Matrix Exponential Function

This is a very interesting function.  The idea is to take the normal exponential function, and put a matrix in its exponent.  The first thing you may be thinking is, "How is that possible?" and the SECOND thing you may be thinking is, "What is the point of doing that?"  Well I hope to answer both these questions in this post.  It IS very strange that we are able to raise e to a matrix, and it is even stranger that this can be useful!

So first thing is first, how the heck can we slap a matrix in the exponential function?  If you recall the Taylor Series expansion (about c=0) it is just a polynomial.  All the operations in the polynomial are legal under matrices, therefore we can replace "x" in the expansion with the matrix "A."

So what is the derivative of this function?  Does it behave in the same way the chain rule does? Let's find out!

So it does indeed behave like the normal chain rule! (Note: do not worry about the nth term in the expansion, since there are an infinite amount of terms, the nth term means nothing.)

So what does this do for us?  If we remember our homogeneous system of linear differential equations...

So amazingly! The matrix exponential function is a solution to the homogeneous system of differential equations!  Let's first try this out on a diagonal matrix A.  This will make the computations very easy.

It turns out that this functions behaves very much like we would expect it to.  Here are properties of the matrix exponential function.

The Cayley-Hamilton Theorem:

The Cayley-Hamilton Theorem basically says that a matrix obeys its characteristic polynomial.  Therefore, if you obtain the polynomial..

Then that means that..

This comes in handy when dealing with systems of differential equations. (Note, the polynomial can be of any form as long as its a polynomial.  I expressed it in this form because that is how we will be using it.)  Unless the matrix A is diagonal, there really is no way of calculating the matrix exponential function unless there are repeated eigenvalues.  If you get repeated eigenvalues, you will have a polynomial of the form shown above.  We can use this in the following way..

Since, A-lambda I will be analogous to the repeated root polynomial, the expansion will terminate after a finite number of terms.  The resulting expression will be equal to the matrix exponential function and the solution to our system.  So in short, use the matrix exponential function when you have repeated eigenvalues!

When a matrix obeys the case of repeated roots, it is said to be nilpotent.  Meaning that it will eventually be the zero matrix if multiplied by itself enough times.

Time for an example!

So this is our characteristic polynomial.  Now we just need to compute the exponential matrix function and find the solution.  ( I am going to write the solution as a fundamental matrix. I will also show that the matrix is nilpotent.)

Notice that it isn't a big deal with the squared term equals zero.  It still follows the Cayley-Hamilton theorem in saying that the cubed term will equal zero.

There is one more topic that I will get to before wrapping this post up.  It deals with the following Lemma.

Let X(t) and Y(t) be two fundamental matricies for the same system x'=Ax.  Then there exists a constant matrix C such that X(t)=Y(t)C.

If you think about it, this makes sense, if you have the solution to the system as X(t), then any other solution will just be a linear combination of the elements in X(t).

We are going to use this fact as a way to calculate e^(At).  If we have the solution to the system x'=Ax, we can write this solution as a fundamental matrix of X(t).  We also know that the exponential matrix function is also a solution to the same system, therefore, by the previous lemma..

Since this is true for any value of t, we use the easy, t=0. We now solve for C.

So in order to compute the exponential matrix function, we need to know the fundamental matrix X(t). Sometimes when dealing with these problems, you may not get enough eigenvectors for each eigenvalue.  This happens when you have multiplicity.  To solve this, we know that (A-λI)u=0, and we know that u is not equal to zero, so then it makes sense that ((A-λI)^k)u=0.  We just multiply both sides by A-λI.  This will produce the required amount of eigenvectors.  (Start with k=1, then 2, then 3, ect until you have enough.)  This method allows us to calculate the matrix exponential function even if we do not have repeated roots!

Heat! A word that is SO commonly misunderstood.

The word heat is vastly misunderstood by the common public and peers of mine studying physics.  I always have to say something when someone says "Delta Q is equal to zero." There is no delta Q! Delta Q doesn't make any sense! (For anyone reading this that isn't mathematically inclined, which I don't know how you got here, delta Q means the change in the amount heat from one time to another.)

The reason behind this is because heat is not a state function. An example of a state function would be internal energy.  As an example, if you have a hot cup of water and a cold one, the hot cup has more internal energy than the colder cup. After a certain amount of time, the hot cup will lose internal energy as it cools, thereby having a specific delta U. (U is internal energy).  This is because at one time, the cup of water possessed a discrete amount of energy, and after a certain amount of time, some of that energy dissipated into the surroundings and now it has less energy.  (Internal energy is defined by the atomic motions of the substance.  When you heat something up, the molecules start to oscillate like crazy.  Internal energy is a measure of these motions, which include but are not limited by, translation, rotation, oscillation, nuclear, ect.)  In fact, when you integrate using heat as the differential, you cannot use a straight dQ, it must be δQ because the integral depends on the path not the state conditions!

This is where the misunderstanding comes in, an object cannot possess heat.  Heat is defined as the transfer of energy, not the amount!  Therefore it is impossible for an object to possess heat because heat is a measure of how much energy is entering or leaving the system.  When the hot water is cooling, the internal energy is being converted into heat because it is leaving the system.  (The system in this case being what is inside the cup.)  You can feel this heat with your hand if you place it over or on the cup.

Sometimes I find that in order to explain something I will purposely use the word heat incorrectly for someone who does not know Physics.  The logic behind this is that they will understand what I am trying to say better than if I were to use internal energy, and then have to explain why the word "heat" is inappropriate.

So! An object cannot possess heat, and delta Q makes no sense!

Solving Non-Homogeneous Systems with Undetermined Coefficients

This works basically the same way as using the method for non-system differential equations.  You just assume the form of the solution and solve for the constants.  The difference this time however, is that the constants are vectors.

For this first example, since the function being added is a constant, we will assume the solution is a constant.  Don't forget to find the homogeneous solution first!

Thats all the time I have for this post. :p

Homogeneous Linear System with Constant Coefficients

So in this post I am going to talk about solving homogeneous linear systems with constant coefficients.  It will be assumed that anyone reading this knows basic vector and matrix operations.  We are going to solve..

As with normal, non system differential equations, the guess for the solution will be an exponential function.

Notice that we need to multiply the exponential by the vector u.  The lambda in the exponential is our old friend the eigenvalue, and the corresponding vector is called the eigenvector.  We MUST multiply the exponential by the eigenvector, otherwise it wouldn't make sense to have a scalar solution to a vector problem.  All we need to do now is plug this into the system.

It is tempting to try and divide by the vector "u" but this CANNOT be done! Division doesn't exist in vectors, it isn't defined!  Notice that we have multiplied the eigenvalue by the identity matrix, this is analogous to multiplying by 1 so we aren't changing anything.  The only reason for doing this was to be able to combine the matrix A with the eigenvalues.  In order to solve this system we first realize that the vector x is not equal to the zero vector, yet the product of x and A-lambda I is equal to zero.  This implies that the matrix A-lambda I is singular which means its determinant is equal to zero.  Therefore the problem is now..

The resulting polynomial is termed the characteristic equation of the matrix.

Solve: (I am just going to show the math with little explanation, as I use this blog as a study tool.)

So what happens if the eigenvalues are complex?  Our old friend Euler's Formula comes into play, just as it did in normal differential equations.  (By normal, I mean non-system.)

So in this next derivation, we will assume the eigenvalues to our system are complex.  Complex numbers always come in pairs remember!  The beauty of this is, when you go to find the eigenvectors, you only need to use one of the complex eigenvalues, the other eigenvector you will get using the other one will just be the conjugate of the first eigenvector.

It can be shown that taking the real part of the imaginary part of this expression (in other words, using the second half without the "i") will also be a solution.  We only used one eigenvector but we would have the same results if we used the other one.  Therefore the two solutions are..

Solve:

Solve:

Notice that we wrote the answer as one matrix called the fundamental matrix.

Nice Properties of Sturm-Liouville Equations

So in my previous post I brought up Sturm-Liouville Equations and mentioned they had nice properties to them.  Also recall that I said you can define the differential operator L[y] anyway you like to.  In this post L[y]=(py')'+qy'.  Which is the Sturm-Liouville definition.

The first important thing to talk about is Lagrange's Identity. This theorem states..

Let u and v be functions having continuous second derivatives on the interval [a,b]. Then,

Where W[u,v] is the Wronskian of the functions u and v.


The value of p in this theorem is always constant.  This can be proved by using Abels Identity on the right hand side of the equation.
To prove this we will  basically use the definition of L[y], the product rule and add and subtract pu'v' simultaneously.

If we integrate both sides we obtain what is known as Green's Formula. 

It can be shown (try it!)  that if the functions u and v satisfy the boundary conditions to the Sturm-Liouville equation, the right hand side is equal to zero.  If we define an inner product as..

Then Greens formula (When it equals zero!) takes the form..

Any operator that satisfies this expression is called a selfadjoint operator.

Okay now on to our next important property of Sturm-Liouville Equations. 

 The Eigenvalues and Eigenfunctions that arise will always be real. 

To prove this we will start out with the Sturm Liouville Equation and take the complex conjugate of both sides. (r(x) is defined to always be real.)

It can be shown that the complex eigenfunction also satisfies the boundary conditions, therefore the complex value of lambda is also an eigenvalue to the problem.  If we take the equation (Before we took the complex conjugate of both sides) and multiplied both sides by the complex eigenfunction and then integrate...

Because both real and complex values of lambda are eigenvalues that give rise to eigenfunctions that satisfy the initial conditions, we can use Greens Formula to obtain..

Therefore we can equate the two expressions and divide out the integral...

Therefore, the only way this can be true is if lambda is real.

If all the eigenvalues are just scalar multiples of one another, then the values are said to be simple.  This leads us to our third important fact.

All eigen values of the regular Sturm-Liouville Eigenvalue problem are simple.

This one isn't that bad to prove.  All you have to do is assume that you have two eigenfunctions corresponding to the same eigenvalue that satisfy the initial conditions.  (The two functions will be Psi and Phi.)

Notice that we solved for the derivatives.  Recall that if the Wronskian is equal to zero, then the two functions are linearly dependent.  This is what we get.

Therefore, the two functions are just scalar multiples of one another.  This means that we essentially only get one eigenfunction for each eigenvalue.

On to the last nice property of Sturm-Liouville Equations!  

All eigenfunctions of these equations will be orthogonal on the interval [a.b].

To prove this, we again assume we have two eigenfunctions except these functions correspond to different  values of lambda.  All we do here is use Greens Formula. (Mu corresponds to another eigenvalue.)

Since lambda does not equal Mu ever, we can conclude that the integral must equal Mu.  Since the integral is the definition of orthogonality, the two eigenfunctions with respect to the weight function r(x), must be orthogonal.