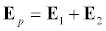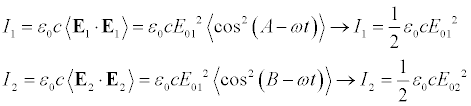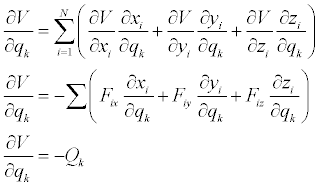Interference of Two Beams

In a previous post, I went over interference of two scalar waves.  We approximated them to be scalar in assuming their paths to point P were nearly parallel.  In this point we no longer have that luxury and we must treat each wave as a vector quantity.

We start by writing down two general equations of plane waves with the same frequency.

Where k=2pi/lambda, s is the distance from the light's respective sources to the point P and phi is the phase constant.  The superposition of these two waves is..

In a previous post I derived the equation for irradiance.  Using that definition..

If we were purely using the particle definition of light we would expect the irradiance would just be I1+I2.  The presence of the third term is an occurrence of the wave nature of light.  This term is deemed the interference term.  We now wish to examine the interference term more closely.  Taking the dot product and using a trigonometric identity..

For purely monochromatic fields, delta is time independent and the average of cosine simply becomes the cosine.  Real fields are not monochromatic and we must be careful when treating this time average.  We can find the irradiance of the two non-interference terms...

Where we have used the fact that the time average of a cosine squared function is 1/2.  This was shown in a previous post.  We can now write the interference term in terms of the two irradiances.

When light comes from two different light sources, the interference term is almost always zero.  This is because no light waves are 100% monochromatic and the time average between these two waves is equal to zero.  The way to represent this is to have phase functions instead of phase constants.  These functions are time dependent.

Beams that follow this are deemed mutually incoherent.    So basically, light beams from different light sources do not interfere with each other.
When the beams originate from the same source and are in phase, they are said to be mutually coherent and the irradiance interference term changes.  Namely, the phi's go to zero.  We will still write delta as the argument however.  Remembering that the cosine function oscillates between -1 and 1, we can get the following relations..

So the irradiance never goes completely to zero unless the two irradiances are equal to one another.  The general form of the irradiance of two beams of equal irradiance is...

Standing Waves, Interference and Group/Phase Velocities

Standing Waves:
When an electromagnetic wave comes into contact with a surface it is reflected.  This phenomenon is analogous to a mechanical wave created in a rope or a sound wave.  The reflected wave travels in the opposite direction with a phase difference.  We can therefore write both waves as..

Notice that the waves are indeed traveling in the opposite direction due to the plus and minus signs in their respective arguments.  Also notice both amplitudes of each wave are the same.  This is because we are modeling the standing wave to have equal amplitudes in both incident and reflective waves.  This means that no energy is absorbed in the reflection process or change in frequency.  If we super impose these two waves, we get... (Using some trigonometry.)

This expression represents the equation for a standing wave where the amplitude of the reflected wave is the same as the incident wave.  It was mentioned earlier that the wave undergoes a phase shift when reflecting off the surface.  It can be shown with Maxwell's Equations that this reflection phase shift is equal to Pi.  Therefore the above equation becomes...

One can interpret this expression as having a spatial dependent amplitude.  Meaning that the amplitude is different at each spot in space.  If we solve this amplitude for when it equals to zero, we can find the spots where the wave always has zero amplitude.  These points are called nodes.

There are also times where the wave is everywhere zero. These waves occur at the times the cosine term is equal to 0.

Similarly we can find the points where the wave is at a maximum and minimum.

If we have two mirrors and have an electromagnetic wave reflecting between them,  In lasers this occurs frequently.  We require the electric field to be equal to zero at each mirror, therefore the space between the mirrors can only hold a certain amount of wave lengths. The distance between the mirrors in terms of the amount of wavelengths between the mirrors is..

Where we have used half the wavelength because the electric field can be zero at a full wave length and a half wavelength.  Solving for wavelength we can find the frequencies of the standing wave modes.

These relations for frequency and wavelengths are strictly for plane mirrors.

Beats:
We now wish to superimpose two waves with the same amplitude, but different frequency.

Where w_p and k_p are the averages of the frequency and proportion constant respectively.  These are much higher than k_g and w_g which occur in the other cosine function.  Therefore one wave is a high frequency wave while the other is a low frequency wave.  The low frequency waves maps out the envelope of their superposition while the high frequency wave traverses in this envelope.  The envelope creates "beats" in the wave which can be used to send information.  The beat frequency is the difference between the two frequency of the two superimposed waves.

Phase and Group Velocity:
The general expression for velocity of a wave is...

The phase velocity is the velocity of the fast frequency wave inside the envelope.  And the group velocity is the velocity of the envelope itself.  Which are..

Where we have used the approximation that w1 is approximately equal to w2 which is approximately equal to w in a small neighborhood.  Same logic for k.  Plugging the phase velocity into the group velocity...

When the velocity does not depend on wavelength such as in a non-dispersive medium.  This would mean the phase and group velocities are zero.  This occurs in vacuum.  In a dispersive medium, v_p=c/n, where n is the refractive index.  The variable n is a function of lambda, meaning a function of k. n(k).

Lagrange's Equations

In physics sometimes it can get annoying remembering formulas for the same physical quantity, but in a different set of coordinates.  It would be very beneficial if we could somehow have a generalized coordinate system that applies to any coordinates we wish to choose.  While in the Cartesian coordinate system we call each coordinate x, y and z, in our generalized coordinate system we shall wall each coordinate q1,q2,q3, ect. So imagine we have a system of particles and we wish to describe the location of each particle.  We are going to write down the coordinates in the generalized coordinate system, which are in terms of the Cartesian coordinate system..

Since these coordinates define the configuration of the system, it must be possible to express each Cartesian coordinate in terms of the general coordinates.

We now obtain the velocities by differentiating with respect to t. 

As an example, here is how you would do this for polar coordinates.

In terms of Cartesian coordinates, the kinetic energy of a system of N particles is..

As an example, we again use plane polar coordinates to show how this works.

As a verification that this is indeed correct, we can start from kinetic energy in Cartesian coordinates and convert it into polar coordinates.

If we were clever enough, we could come up with a logic that justifies this formula for kinetic energy without starting from the Cartesian coordinates.  However, using this method is dangerous because if the coordinates being used are not orthogonal, then the cross terms will not cancel out as they did in the above example for polar coordinates.

Notice that the components of linear momentum of the particle are..

(THE MIDDLE TERM SHOULD HAVE AN EQUAL SIGN BETWEEN "m*y" AND THE PARTIAL DERIVATIVE.)

Also notice that our previous expression for kinetic energy in polar coordinates yields the momentum if we take the derivative.

A similar relationship can be shown for cylindrical and spherical coordinates in three dimensions.  This suggests that we can find a generalized momentum expression for any coordinate system.

If q is a quantity that measures distance, then this expression corresponds to linear momentum, and if q measures an angle this expression corresponds to the angular momentum.  In other cases where the coordinate system may not define a distance or an angle, this expression represents something of physical significance.

Using our generalized expression for kinetic energy, the generalized momentum is..

We now wish to determine the generalized force.  Imagine you have a system of particles, and each particle is acted on by a different force.  The total work done on the particles is while each particle moves a small incremental amount is..

The incremental distances can be expressed as..

Substituting these expressions into the definition for work..

Where Q is the generalized force associated with q_k.  If the general force is derivable from a potential energy function, then..

If V is expressed in terms of the generalized coordinates..

We came to this conclusion by comparing the two expressions for the work.  This can also be verified by direct computation of the derivatives of the potential function.

We will not calculate the generalized forces associated with polar coordinates. Using the definition of Q...

So in the r direction we have the force in the direction of r, and in the theta direction we have the torque.  In general, if q_k is a coordinate that measures distance, F_k will be the component of the total force acting in that direction and if q_k is a coordinate that measures an angle, then the resulting force is the torque in that angular direction.

Our analysis of generalized momentum and force lead us to believe there could be a generalized equation of motion.    The time rate of change of momentum is..

Starting with Newtons Equations of motion in Cartesian form.

The kinetic energy, staring in Cartesian coordinates is..

Next we differentiate the following relations from earlier..

Substituting these into our previous equation for kinetic energy, then differentiating again with respect to t we obtain...

According to Newtons second Law the first term is..

But remember that this just equals Q_k.

The derivatives for the second term go like this..

Where we used the same relations for x(dot) again in the last step.  So this the last term is..

Therefore, our expression for the change in momentum is...

So our original guess for the change in momentum was not entirely correct.  We see that we must add the generalized force Q_k.  What is the physical significant of the right hand side of this equation?  Well, in polar coordinates..

And the equation of motion in polar coordinates is..

Therefore we see that the derivative with respect to r of the kinetic energy is actually part of "mass times acceleration" transposed to the other side and is not technically a force if you remember.  We can re-write our equation for the rate of change of momentum in a more standard form..

These equations are called Lagrange's Equations.  If a potential energy exists so that Q_k is derivable from it, we can introduce the Lagrangian Function, L.  

Where we have used the fact that the derivative of the potential function with respect to the coordinates is the force, and the fact that T depends on both the coordinates and their velocities, while V only depends on the coordinates. (For the first derivative, dV/dq(dot) =0)

Using Lagrange's Equations, we can arrive at the Newtonian equations of motion.  Consider a system of particles 1 to N. 

Working in planar polar coordinates (2D), we can obtain the equations of motion as well with the Lagrange's Equations.

t