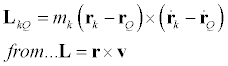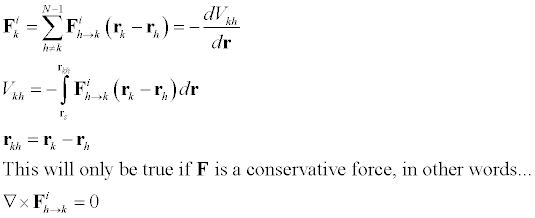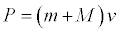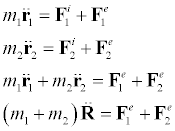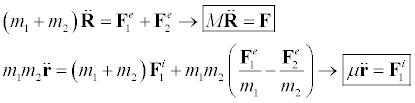The Motion of a System of Particles

THESE NOTES, AS WELL AS THE MOTION OF A PARTICLE IN 2 AND 3 DIMENSIONS WERE TAKEN FROM THE BOOK "MECHANICS: THIRD EDITION BY SYMON"

In this section, we're going to talk about forces, and their responsive motions of a system of particles, such as modeling an atomic lattice.  If we have a particle, then the force acting upon this "kth" particle, will be the sum of the internal forces on particle k by all the other N-1 particles, plus any external force which may be applied to particle k. The superscript "e" will designate external forces and the superscript "i" will designate internal forces.  This the equation of motion for any particle is..

Using the definition of linear momentum and then summing both sides of the equation over N, we can re-write this equation as...

We now make the assumption that the sum of the internal forces in the system is equal to zero.  Let us justify this claim.  Using Newtons third law, we know that any forces acted on by h on to particle k will invoke a response in particle k that creates the negative of the force of particle h.  In other words...

So to take care of all these interactions between the internal particles, we can re-write the expression for the internal forces using a double sum.

This expression will contain terms of forces acting upon k by h, and forces acting upon h by k.  Summing all these up will equal zero.  As an example, we will use a system of three particles.

So using this fact, we can re-write out equation of motion as..

This is newtons second law for a system of particles.  Where we have denoted capital P as the sum of all the momentum in the system.  We can now come to an important fact if we introduce the concept of center of mass.  The expression for the center of mass is..

We now realize that the total momentum can be written as...

This brings us to the very important consequence.

Thus, we can treat a system of particles as ONE particle at its center of mass!

We now move our conversation to analyzing the vector angular momentum of a particle k in a system.  The angular momentum of particle k about a point Q not necessarily the origin is... (Remember! Angular momentum has a different value bases on where the point Q is!)

Differentiating this and substituting the definition of  linear momentum in..

The total angular momentum and the total external torque about the point Q are...

Summing the expression for the derivative of the angular momentum over all the particles we obtain...

When the point Q is at rest or traveling at a constant velocity, then the last term on the right is equal to zero.  We will assume this is the case as the most important cases occur when Q is the origin and thus, isn't moving. 

The first term is the total internal torque.  If we assume this is equal to zero then the expression becomes...

This is the angular momentum theorem for a system of particles.

We now endeavor to prove that the internal torque will in fact be equal to zero.  To do this we must assume newtons third law in the strong form.  Meaning, not only do the forces come in pairs, but the forces act in the same line between the particles. (This should make sense!)  We can write the internal torque term as..

By the strong form of Newtons third law, both the vectors in the final double sum act along the same line and thus their cross product is equal to zero.  Thereby proving that the internal torque is equal to zero.

In many cases the total force acting on any particle in a system of particles depends only on the positions of the particles in the system.  That means we can re-write the force in the equation of motion as..(As well as doing some manipulations..)

We once again have derived the conservation of energy.  If the internal forces are derivable from a potential energy function V but the external forces are not, then this theorem look like...

Suppose that the internal force acting on any particle k can be regarded as the sum of the forces due to each of the other particles, where the force on the kth particle due to the hth particle only depends on the relative position of the particle k with respect to h.  This means that a potential energy function may in fact exist for the internal forces as well.

If Newtons third Law holds (Weak form) then....

This V_(kh) will also serve as the potential energy function for the force on particle h by k.  We can now define the total internal potential energy V for the system of particles as the sum of V_(kh) over all the pairs of particles.

The conservation laws are very important in Physics.  One example of the conservation of linear momentum is the conveyor belt problem.  A hopper above a conveyor belt is dropping material onto the conveyor belt.  What is the force needed to keep the conveyor belt moving at a constant velocity?

The total momentum of the system, which includes the belt plus the material on the belt and in the hopper is..

Where M is the mass of the belt and m is the mass of the material.  Using the linear momentum theorem (Newtons second Law for a system of particles) we can find the force and the power on the belt.

Remember, v is constant here, the quantity that is changing is the mass "m."  Notice that this power, is twice the rate at which the kinetic energy is increasing. 

Conservation laws are very useful when studying collisions of particles.  The initial and final linear momentum of both particles in the collision added up must be the same value.  The same concept applied for the kinetic energy of each particle.

If one particle is at rest, after the collision each particle will shoot off in a different direction to the initial contact point.

We will now do the following manipulations to get rid of theta 2.

From these solutions, we can find the final momentum of either particle.

We now shift our focus from collisions to the two body problem.  Take two particles under external forces, and internal forces, where the internal forces are the forces one particle acts upon the other.  The equation of motion for the two particles are..

We will now do a chance of coordinates.

The inverse transformation is..

(ERROR!: The numerator in the r1 term should have m2 NOT m1!!)

In this system, R is the coordinate of the center of mass, and r is the relative coordinate of mass 1 with respect to mass 2.  Adding the two original equations of motion and using Newtons third law on the internal forces..

Doing the following manipulations we can find an equation of motion for r.

We will now assume that..

And now we will use the following definitions.

The equations of motion now become..

"The first equation is the center of mass equation of motion obtained earlier.  The second equation is the equation of motion for a particle of mass Mu, acted on by the internal force F1 that particle 2 exerts on particle 1.  Thus the motion of particle 1 as viewed from particle 2 is the same as if particle 2 were fixed and particle 1 had a mass of Mu.  If one particle is much heavier than the other, Mu is slightly less than the mass of the lighter particle.  If the particles are of equal mass, Mu is half the mass of either. We can apply this principle to the gravitational force provided the external forces are either zero or are proportional to the masses as we assumed." Direct quote from Mechanics Third Edition by Symon, pg. 184, 1st paragraph.

Using this method, a two body problem can be reduced to a one body problem.  This coordinate system is very convenient by the fact that the problem obtains very nice properties.  One such property is that the total linear momentum is equal to zero.  We will not prove this fact.  

In reference to the center of mass between the two objects,  object 1 and 2 are on either side of the center of mass.  Object 1 is defined by a vector from itself to the center of mass, and object 2 is defined by a vector from the center of mass to itself, by inspection of the vectors it is clear that...

Thus we have proved that the total linear momentum in center-of-mass coordinates is always equal to zero.  Another useful property of these coordinates is that in the absence of external forces, the center of mass always travels with constant velocity.

Where we have used the fact that there are no external forces acting on the center of mass.

I mentioned earlier that when we have a two body problem, we can convert it into a one body problem by changing the coordinates with respect to the center of mass.  What shall we then do when we have an N-body problem?  It normally does not work so nicely and I cannot just say that we can reduce a three body problem to a simpler set up because it just isn't that way many times.  The method we are about to do is to first find the motion of the center of mass and then find the internal motion of the system, namely the motion of its particles relative to the center of mass.  We will now define a coordinate vector of the kth particle as the vector from the center of mass to the kth particle.

The terms with a superscript "i" represent the internal coordinates.  Because we are in the center of mass coordinates, the following relationship must be true.

The center of mass velocity and the internal velocities are..

From the above summation, we can show the total linear momentum is equal to zero.

The total kinetic energy is the system is..

The total angular momentum about the origin is..

Notice how the angular momentum depends on the internal coordinates and velocities and is independent of the origin in which it is rotated.  Notice how both the kinetic energy and angular momentum are dependent on the motion of the center of mass and the internal coordinates.

Wave Equations

One Dimensional Wave Equation
In Physics waves show up everywhere, therefore it is necessary that we develop a mathematical representation of these waves.  The most basic type of wave is the one dimensional traveling wave.  Imagine we have an equation of a wave that is a frozen snapshot.  We define some arbitrary point P that is on the wave and we will call this coordinate system the O coordinate system.  This wave has the very general expression..

If we allow the wave to move a certain amount of distance, the point P is now a distance of x=vt away from where it originally was.  The point P can now be described in either coordinate system as (x,y) or (x+vt,y).  Notice how the y component is the same in each system since this wave is moving horizontally.  We now express the function y in these new coordinates.

Where we have introduced a minus sign to take care of the situation when the wave moves in the opposite direction, and the notation x' to equal x+vt or x-vt.  Any function of this form represents a traveling wave, it need not be a sinusoidal function.  All the following examples represent traveling waves.

Our goal now is to set up a partial differential equation that describes a wave despite what y is actually equal to.
In this model, we are assuming constant velocity.

If we are talking about light, v=c which is the speed of light.  In order to see if a function is a traveling wave, you either try to look for x+vt or see if it satisfies this partial differential equation.

Harmonic Waves
A very important type of wave is a harmonic wave.  These type of waves are described either the sine or cosine function and have a periodic and endless nature to them.

Since the both of these functions are the same except shift a distance of pi/2 radians, we need only develop relations for one of them because the relation can immediately be applied to the other.  In this post, we will use the sine function.
Imagine you have a sine wave in the x,y plane.  This will be a snap shot of the wave so t is equal to a constant.  From peak to peak on the graph represents the wavelength of the wave (since the horizontal axis is spatial).  Wavelength is represented by the Greek letter lambda. If the wave moves a distance of lambda, then the same point can be described by shifting the x component a distance of lambda this type of movement is described also by adding 2pi in the sine argument. In other words..

We can now find an expression for k.

This is deemed the propagation constant and contains information about the wavelength.  The same logic from above can be done in the t,y plane with a constant position. The only difference is that the distance from peak to peak is no longer the wavelength.  Since the horizontal axis is time, this distance describes the period of the wave.

Combining these two expression we get a very familiar formula.

Where we have used the relation frequency=1/Period. Combining these first two expressions into the sine expression we come up with the general relation that is used for a wave.

Where we have deemed the expression 2pi*f equal to omega.  Omega is termed the angular frequency.  This is mainly because its units are inverse seconds and is simply done to make the expression for a wave look simpler.
If x and t vary in a way such that the whole argument of the sine or cosine function is constant, it describes a situation of a plane wave, or wave front.  And we can see that..

This confirms that v represents the wave velocity.  Notice however the signs are flipped,  meaning the wave is moving in the positive direction then the expression x-vt is seen and vice versa.
Many times dues to initial conditions, we might not want to start looking at the wave directly from its "start" but rather shifted to the initial point of interest.  In these situations we simply add what is known as a "phase constant" to move the sine function to our interested starting point.

It is sometimes very useful to represent these wave equations in the complex plane. (See my post on complex numbers for more details.)  An expression that can either be the sine or cosine function is..

So depending on which trigonometric function we are using, we can either use the real or imaginary part of y. 

We now want to elaborate more no the notion of plane waves.  Firstly, we want a plane wave to describe a wave in all three coordinates, not just in the x direction.  For three dimensions, the wave equations looks like..

Note that k is now a vector, the k vector is pointing in the direction of propagation of the wave.  In complex form, the general expression for a wave is..

The partial differential equation associated with all three dimensions is..

Electromagnetic Waves

Electromagnetic waves have the same form as a sinusoidal wave.  In this case, the amplitude A represents the amplitude of either the electric or magnetic field.  Recall that light is simply the oscillation of electric and magnetic fields perpendicular to one another.

We start this section by showing Maxwell's Equations in free space in the differential form.

If we take the cross product of the third equation, and use the others during the derivation we obtain..

Note that the vector identity we used in the first step can be proved using the Levi-Cevita symbol.  If you do not know what this is, don't worry about it.  That particular proof isn't terribly important in this case. 

Notice that we ended up with a wave equation.  This is how light was deduced to be a wave.  We then related this expression to our earlier definition of a wave and found an expression to represent the speed of light.  A very similar proof can be done for the magnetic field by taking the curl of equation 4.

The energy density associated with the electric field and magnetic field in free space are..

The energy is therefore divided equally between the two fields, and the total energy density is given by..

We now consider the rate at which the electromagnetic wave delivers energy, or its power. In a certain time delta(t) the energy transported through a cross section of area A is the energy associated with the volume delta(V) of a rectangular volume of length c*delta(t), where c is the speed of light.  

We will now express the energy density u in terms of E and B.

When the power per unit area, is assigned the direction of propagation, it is called the Poynting vector.  The direction of propagation is equal to the cross product of the E and B fields. (Why?)

Since E and B are changing extremely rapidly, S is also changing very rapidly, not in direction however in magnitude. What we need to do now is take the time average of the amount of energy given by the Poynting vector.  This average is energy is called the irradiance.