Laplace's Equation in Spherical coordinates is...
In order for three functions of three different variables to equal a constant, they must each themselves be equal to a constant.
Getting back to the main differential equation, we will do some re-arranging and use n(n+1) as the separation constant.
Let us now solve the equation for U. This is a Cauchy-Euler Equation.
We now return to the main differential equation.
This is the generalized Legendre equation.
We will assume azimuthal symmetry (aka, no dependence on r, aka axial symmetry) this means that m=0 and we are left with the ordinary Legendre Equation.
We will now solve this differential equation using a series solution.
We now have a recursive relation to generate the other coefficients.
These are the Legendre Polynomials.
We need to normalize each polynomial so that its value is unity for x=1.
Let us calculate a couple of the polynomials. You will notice that for even values of n, the first term terminates while the other term doesn't. (Likewise for odd values of n and the other series.) We only need one of them for a solution so we will take the one that terminates.
The Legendre Polynomials can be put into closed form..
But don't forget! We still need to solve for V in our original equation by plugging everything in. Remember we are still assuming azimuthal symmetry. (m=0)

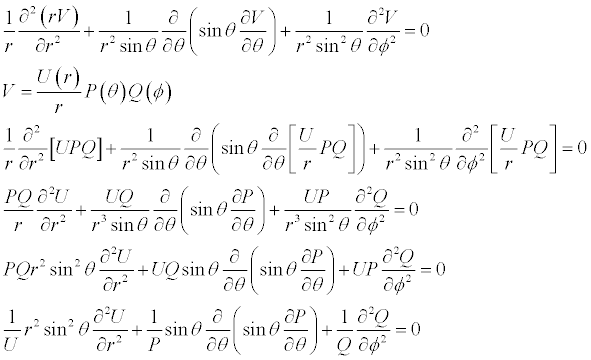












No comments:
Post a Comment