Since these coordinates define the configuration of the system, it must be possible to express each Cartesian coordinate in terms of the general coordinates.
We now obtain the velocities by differentiating with respect to t.
As an example, here is how you would do this for polar coordinates.
In terms of Cartesian coordinates, the kinetic energy of a system of N particles is..
As an example, we again use plane polar coordinates to show how this works.
As a verification that this is indeed correct, we can start from kinetic energy in Cartesian coordinates and convert it into polar coordinates.
If we were clever enough, we could come up with a logic that justifies this formula for kinetic energy without starting from the Cartesian coordinates. However, using this method is dangerous because if the coordinates being used are not orthogonal, then the cross terms will not cancel out as they did in the above example for polar coordinates.
Notice that the components of linear momentum of the particle are..
(THE MIDDLE TERM SHOULD HAVE AN EQUAL SIGN BETWEEN "m*y" AND THE PARTIAL DERIVATIVE.)
Also notice that our previous expression for kinetic energy in polar coordinates yields the momentum if we take the derivative.
A similar relationship can be shown for cylindrical and spherical coordinates in three dimensions. This suggests that we can find a generalized momentum expression for any coordinate system.
If q is a quantity that measures distance, then this expression corresponds to linear momentum, and if q measures an angle this expression corresponds to the angular momentum. In other cases where the coordinate system may not define a distance or an angle, this expression represents something of physical significance.
Using our generalized expression for kinetic energy, the generalized momentum is..
We now wish to determine the generalized force. Imagine you have a system of particles, and each particle is acted on by a different force. The total work done on the particles is while each particle moves a small incremental amount is..
The incremental distances can be expressed as..
Substituting these expressions into the definition for work..
Where Q is the generalized force associated with q_k. If the general force is derivable from a potential energy function, then..
If V is expressed in terms of the generalized coordinates..
We came to this conclusion by comparing the two expressions for the work. This can also be verified by direct computation of the derivatives of the potential function.
We will not calculate the generalized forces associated with polar coordinates. Using the definition of Q...
So in the r direction we have the force in the direction of r, and in the theta direction we have the torque. In general, if q_k is a coordinate that measures distance, F_k will be the component of the total force acting in that direction and if q_k is a coordinate that measures an angle, then the resulting force is the torque in that angular direction.
Our analysis of generalized momentum and force lead us to believe there could be a generalized equation of motion. The time rate of change of momentum is..
Starting with Newtons Equations of motion in Cartesian form.
The kinetic energy, staring in Cartesian coordinates is..
Next we differentiate the following relations from earlier..
Substituting these into our previous equation for kinetic energy, then differentiating again with respect to t we obtain...
According to Newtons second Law the first term is..
But remember that this just equals Q_k.
The derivatives for the second term go like this..
Where we used the same relations for x(dot) again in the last step. So this the last term is..
Therefore, our expression for the change in momentum is...
So our original guess for the change in momentum was not entirely correct. We see that we must add the generalized force Q_k. What is the physical significant of the right hand side of this equation? Well, in polar coordinates..
And the equation of motion in polar coordinates is..
Therefore we see that the derivative with respect to r of the kinetic energy is actually part of "mass times acceleration" transposed to the other side and is not technically a force if you remember. We can re-write our equation for the rate of change of momentum in a more standard form..
These equations are called Lagrange's Equations. If a potential energy exists so that Q_k is derivable from it, we can introduce the Lagrangian Function, L.
Where we have used the fact that the derivative of the potential function with respect to the coordinates is the force, and the fact that T depends on both the coordinates and their velocities, while V only depends on the coordinates. (For the first derivative, dV/dq(dot) =0)
Using Lagrange's Equations, we can arrive at the Newtonian equations of motion. Consider a system of particles 1 to N.
Working in planar polar coordinates (2D), we can obtain the equations of motion as well with the Lagrange's Equations.
t
















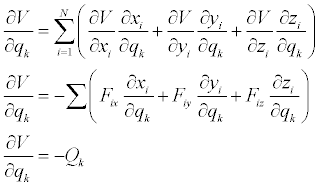
















No comments:
Post a Comment