In a previous post, I went over interference of two scalar waves. We approximated them to be scalar in assuming their paths to point P were nearly parallel. In this point we no longer have that luxury and we must treat each wave as a vector quantity.
We start by writing down two general equations of plane waves with the same frequency.
Where k=2pi/lambda, s is the distance from the light's respective sources to the point P and phi is the phase constant. The superposition of these two waves is..
In a previous post I derived the equation for irradiance. Using that definition..
If we were purely using the particle definition of light we would expect the irradiance would just be I1+I2. The presence of the third term is an occurrence of the wave nature of light. This term is deemed the interference term. We now wish to examine the interference term more closely. Taking the dot product and using a trigonometric identity..
For purely monochromatic fields, delta is time independent and the average of cosine simply becomes the cosine. Real fields are not monochromatic and we must be careful when treating this time average. We can find the irradiance of the two non-interference terms...
Where we have used the fact that the time average of a cosine squared function is 1/2. This was shown in a previous post. We can now write the interference term in terms of the two irradiances.
When light comes from two different light sources, the interference term is almost always zero. This is because no light waves are 100% monochromatic and the time average between these two waves is equal to zero. The way to represent this is to have phase functions instead of phase constants. These functions are time dependent.
Beams that follow this are deemed mutually incoherent. So basically, light beams from different light sources do not interfere with each other.
When the beams originate from the same source and are in phase, they are said to be mutually coherent and the irradiance interference term changes. Namely, the phi's go to zero. We will still write delta as the argument however. Remembering that the cosine function oscillates between -1 and 1, we can get the following relations..
So the irradiance never goes completely to zero unless the two irradiances are equal to one another. The general form of the irradiance of two beams of equal irradiance is...

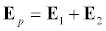


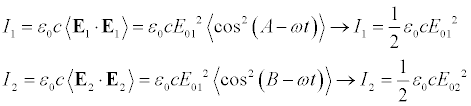




No comments:
Post a Comment