In Physics waves show up everywhere, therefore it is necessary that we develop a mathematical representation of these waves. The most basic type of wave is the one dimensional traveling wave. Imagine we have an equation of a wave that is a frozen snapshot. We define some arbitrary point P that is on the wave and we will call this coordinate system the O coordinate system. This wave has the very general expression..
If we allow the wave to move a certain amount of distance, the point P is now a distance of x=vt away from where it originally was. The point P can now be described in either coordinate system as (x,y) or (x+vt,y). Notice how the y component is the same in each system since this wave is moving horizontally. We now express the function y in these new coordinates.
Where we have introduced a minus sign to take care of the situation when the wave moves in the opposite direction, and the notation x' to equal x+vt or x-vt. Any function of this form represents a traveling wave, it need not be a sinusoidal function. All the following examples represent traveling waves.
Our goal now is to set up a partial differential equation that describes a wave despite what y is actually equal to.
In this model, we are assuming constant velocity.
If we are talking about light, v=c which is the speed of light. In order to see if a function is a traveling wave, you either try to look for x+vt or see if it satisfies this partial differential equation.
Harmonic Waves
A very important type of wave is a harmonic wave. These type of waves are described either the sine or cosine function and have a periodic and endless nature to them.
Since the both of these functions are the same except shift a distance of pi/2 radians, we need only develop relations for one of them because the relation can immediately be applied to the other. In this post, we will use the sine function.
Imagine you have a sine wave in the x,y plane. This will be a snap shot of the wave so t is equal to a constant. From peak to peak on the graph represents the wavelength of the wave (since the horizontal axis is spatial). Wavelength is represented by the Greek letter lambda. If the wave moves a distance of lambda, then the same point can be described by shifting the x component a distance of lambda this type of movement is described also by adding 2pi in the sine argument. In other words..
We can now find an expression for k.
This is deemed the propagation constant and contains information about the wavelength. The same logic from above can be done in the t,y plane with a constant position. The only difference is that the distance from peak to peak is no longer the wavelength. Since the horizontal axis is time, this distance describes the period of the wave.
Combining these two expression we get a very familiar formula.
Where we have used the relation frequency=1/Period. Combining these first two expressions into the sine expression we come up with the general relation that is used for a wave.
Where we have deemed the expression 2pi*f equal to omega. Omega is termed the angular frequency. This is mainly because its units are inverse seconds and is simply done to make the expression for a wave look simpler.
If x and t vary in a way such that the whole argument of the sine or cosine function is constant, it describes a situation of a plane wave, or wave front. And we can see that..
This confirms that v represents the wave velocity. Notice however the signs are flipped, meaning the wave is moving in the positive direction then the expression x-vt is seen and vice versa.
Many times dues to initial conditions, we might not want to start looking at the wave directly from its "start" but rather shifted to the initial point of interest. In these situations we simply add what is known as a "phase constant" to move the sine function to our interested starting point.
It is sometimes very useful to represent these wave equations in the complex plane. (See my post on complex numbers for more details.) An expression that can either be the sine or cosine function is..
So depending on which trigonometric function we are using, we can either use the real or imaginary part of y.
We now want to elaborate more no the notion of plane waves. Firstly, we want a plane wave to describe a wave in all three coordinates, not just in the x direction. For three dimensions, the wave equations looks like..
Note that k is now a vector, the k vector is pointing in the direction of propagation of the wave. In complex form, the general expression for a wave is..
The partial differential equation associated with all three dimensions is..
Electromagnetic Waves
Electromagnetic waves have the same form as a sinusoidal wave. In this case, the amplitude A represents the amplitude of either the electric or magnetic field. Recall that light is simply the oscillation of electric and magnetic fields perpendicular to one another.
We start this section by showing Maxwell's Equations in free space in the differential form.
If we take the cross product of the third equation, and use the others during the derivation we obtain..
Note that the vector identity we used in the first step can be proved using the Levi-Cevita symbol. If you do not know what this is, don't worry about it. That particular proof isn't terribly important in this case.
Notice that we ended up with a wave equation. This is how light was deduced to be a wave. We then related this expression to our earlier definition of a wave and found an expression to represent the speed of light. A very similar proof can be done for the magnetic field by taking the curl of equation 4.
The energy density associated with the electric field and magnetic field in free space are..
The energy is therefore divided equally between the two fields, and the total energy density is given by..
We now consider the rate at which the electromagnetic wave delivers energy, or its power. In a certain time delta(t) the energy transported through a cross section of area A is the energy associated with the volume delta(V) of a rectangular volume of length c*delta(t), where c is the speed of light.
We will now express the energy density u in terms of E and B.
When the power per unit area, is assigned the direction of propagation, it is called the Poynting vector. The direction of propagation is equal to the cross product of the E and B fields. (Why?)
Since E and B are changing extremely rapidly, S is also changing very rapidly, not in direction however in magnitude. What we need to do now is take the time average of the amount of energy given by the Poynting vector. This average is energy is called the irradiance.










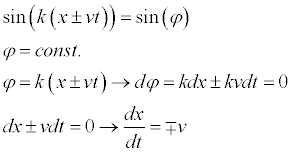













No comments:
Post a Comment