So first thing is first, how the heck can we slap a matrix in the exponential function? If you recall the Taylor Series expansion (about c=0) it is just a polynomial. All the operations in the polynomial are legal under matrices, therefore we can replace "x" in the expansion with the matrix "A."
So what is the derivative of this function? Does it behave in the same way the chain rule does? Let's find out!
So it does indeed behave like the normal chain rule! (Note: do not worry about the nth term in the expansion, since there are an infinite amount of terms, the nth term means nothing.)
So amazingly! The matrix exponential function is a solution to the homogeneous system of differential equations! Let's first try this out on a diagonal matrix A. This will make the computations very easy.
It turns out that this functions behaves very much like we would expect it to. Here are properties of the matrix exponential function.
The Cayley-Hamilton Theorem:
The Cayley-Hamilton Theorem basically says that a matrix obeys its characteristic polynomial. Therefore, if you obtain the polynomial..
Then that means that..
This comes in handy when dealing with systems of differential equations. (Note, the polynomial can be of any form as long as its a polynomial. I expressed it in this form because that is how we will be using it.) Unless the matrix A is diagonal, there really is no way of calculating the matrix exponential function unless there are repeated eigenvalues. If you get repeated eigenvalues, you will have a polynomial of the form shown above. We can use this in the following way..
Since, A-lambda I will be analogous to the repeated root polynomial, the expansion will terminate after a finite number of terms. The resulting expression will be equal to the matrix exponential function and the solution to our system. So in short, use the matrix exponential function when you have repeated eigenvalues!
When a matrix obeys the case of repeated roots, it is said to be nilpotent. Meaning that it will eventually be the zero matrix if multiplied by itself enough times.
Time for an example!
So this is our characteristic polynomial. Now we just need to compute the exponential matrix function and find the solution. ( I am going to write the solution as a fundamental matrix. I will also show that the matrix is nilpotent.)
Notice that it isn't a big deal with the squared term equals zero. It still follows the Cayley-Hamilton theorem in saying that the cubed term will equal zero.
There is one more topic that I will get to before wrapping this post up. It deals with the following Lemma.
Let X(t) and Y(t) be two fundamental matricies for the same system x'=Ax. Then there exists a constant matrix C such that X(t)=Y(t)C.
If you think about it, this makes sense, if you have the solution to the system as X(t), then any other solution will just be a linear combination of the elements in X(t).
We are going to use this fact as a way to calculate e^(At). If we have the solution to the system x'=Ax, we can write this solution as a fundamental matrix of X(t). We also know that the exponential matrix function is also a solution to the same system, therefore, by the previous lemma..
Since this is true for any value of t, we use the easy, t=0. We now solve for C.
So in order to compute the exponential matrix function, we need to know the fundamental matrix X(t). Sometimes when dealing with these problems, you may not get enough eigenvectors for each eigenvalue. This happens when you have multiplicity. To solve this, we know that (A-λI)u=0, and we know that u is not equal to zero, so then it makes sense that ((A-λI)^k)u=0. We just multiply both sides by A-λI. This will produce the required amount of eigenvectors. (Start with k=1, then 2, then 3, ect until you have enough.) This method allows us to calculate the matrix exponential function even if we do not have repeated roots!





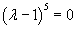




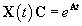

No comments:
Post a Comment