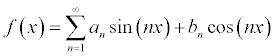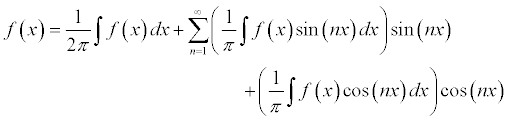Orthogonal Functions ,Fourier Series and Fourier Transforms

Any topic that has Fourier series should include a discussion of orthogonal functions.  The concept of orthogonal functions may sound strange at first.  Surely you know you can have orthogonal vectors, meaning they are perpendicular to each other.  If we say two functions are orthogonal are we saying anything about their geometrical relation to each other?  Not exactly no.  The term "orthogonal function" comes from the parallel in relating functions to vectors.  If you have two vectors A and B, then they are orthogonal if their dot product is equal to zero.  Namely..

If we have two functions that, when multiplied together at a point, equal zero then just by analogy we say these functions are orthogonal at that point.

Note how when working with vectors, the dot product of two vectors is..

Likewise, when working with functions, if we want to see if two functions are orthogonal at every point then we must do the same thing.  Firstly we will take values in discrete intervals.

If we allow delta x to approach zero, then we turn this discrete sum into a continuous sum and the summation becomes the integral.  Remember that we want to incorporate the entire real line so the summation / integral must go from negative infinity to positive infinity.

This is the test for orthogonality of functions over the entire real line.  Orthogonal functions are very useful in Fourier series.

Recall from Taylor series, that the goal was to write a function in terms of an infinite power series, or polynomial.  The goal for Fourier series is the same except we are no longer working with polynomials, but this time with sine and cosine functions.

For any function f(x) you can write its series expansion as the following...

        (1)

The terms in the arguments may seem arbitrary but they will be explained shortly.  The question may arise in your head, "Why sine and cosine and not another type of function?"  The answer to that is because sine and cosine are orthogonal in to each other in certain intervals and we exploit this in the following way.

Imagine we start out with just sine and cosine functions with an argument of just "x."

    (2)

This would be our initial attempt if we had no idea how to do this.  Note that the arguments must be "nx" so that we have a sum of different sine terms.  Much like the exponent in a Taylor series has to be n.  The interval we will have will be from -pi to +pi.  If we multiply (2) by cos(mx)  (Note that m need not be the same as n.) and then integrate both sides we get...

The left hand side remains as it is as no other simplification can occur, the right hand side however is a different story.  We have two types of integrals with 3 conditions each.

Let's start with the second one and do each case.  (The integration will be shown but not explained.  However, concepts will be explained.)

The first integral is evaluated in much the same manner.

So it looks like our equation simplifies to..

So we have found all the "b" coefficients in our Fourier series.  To find all the "a" components we do the simply multiple (2) by sin(mx) instead and do the same thing.  One of the integrals we have already done so we need not do the work again.

So (2) reduces to..
Thus, the final expression for the Fourier series can be written as..

(The limits on the first term should be -pi to pi as are the limits for the coefficients.)

A little experimenting will show that these trigonometric functions are not orthogonal for general regions.  It would be nice to have an expression that accounts for any range, not just between negative pi and pi.  To do this you simply impose the condition in the arguments of the functions to be zero at the end of the interval.  If we have an interval between -L and L then the Fourier series would be..

(The limits on the first term should be -L to L as are the limits for the coefficients.)

While our three different integrals from before will become.. (Notice that we use their symmetry to rewrite the limits in two of the cases.

Based on the work we just did, you shouldn't need too much convincing to realize that these are in fact correct.  As a very simple example, let us find the Fourier series of 1 over the interval [0,10].

Here is a graph for about 10 or so terms.

As the number of terms go to infinity, the curve of the Fourier zeroes will grow ever closer to 1 (the blue line).  If you were to graph this yourself you will notice it repeats after a period of 10.  It is also symmetric about the origin.  This is because the function is odd.

We can also formulate a complex form of the Fourier Series.  We assume we can write the function f(x) as..

And we want to find this over the interval [-L,L].  In much the same was as we did previously..

Notice that we can include the first term c_0 in the general term for c_n because e^0=1.  The final complex Fourier Series is..

Much simpler looking than its trigonometric counterpart!
One question might arise in your head, and that is, "Can we extend the interval of the Fourier Series to accommodate the entire real line?"  This would mean the graphical representation is no longer periodic and the entire function is transformed into another space.  We will first make the following definitions..

This expression for f(x) looks very similar to the fundamental theorem of calculus! If we let delta k approach zero, namely let L approach infinity, then we have..

This is the Fourier Transform.  Finding g(k) is analogous to finding c_n in the Fourier Series.  This is what is known as an integral transform.  Note that the 1/2pi can be put in either f(x) or g(k).  It can also have a factor of sqrt(1/2pi) in each one.
Using Euler's formula we can rewrite this transform as..

(Note that we are using a dummy variable u.  It could just as well be x!)

If the function we are trying to transform is odd, then the product f(u)cos(ku) is odd and any even function integrated over a symmetric interval is zero.  Then we get..

This is the Fourier Sine transform.  In a similar way we can get the Fourier Cosine Transform.

The Fourier Sine transform is used to represent odd functions and the Fourier Cosine transform is used to represent even functions.

Let us transform the following function using a Fourier Transform.

We thus have an integral representation of the original function.
The final topic of this post if the concept of convolution.  To introduce this topic, convolution will first be shown with Laplace transforms and then the concept will be extended into Fourier Transforms.

Imagine we are solving a differential equation and we have the following transform made..

In stead of taking partial fractions, there is another way to get the inverse Laplace transform. We are going to explore the possibility of taking the inverse Laplace transform of a product of Laplace transforms.  If we take the above expression to be G(r)H(r) we can plug this into the definition for a Laplace transform and make a change of variables.

We now want to switch the limits of integration.  When sigma equals 0, t=T.  If you draw this in a plane, the limits of integration goes from zero to t=T which is a straight line in the plane.  Making the geometrical interpretation you obtain the following result.

We can now use this on the original problem.  It goes however, involve us finding the inverse laplace transform of each factor. (The integral in the brackets is called a convolution integral.)

We now extend this concept into Fourier Transforms.  The work is very similar.  We once again have a product of two Fourier Transforms and wish to inverse the transformation.  We once again do a change of variables and get a convolution integral.

Interference of Two Beams

In a previous post, I went over interference of two scalar waves.  We approximated them to be scalar in assuming their paths to point P were nearly parallel.  In this point we no longer have that luxury and we must treat each wave as a vector quantity.

We start by writing down two general equations of plane waves with the same frequency.

Where k=2pi/lambda, s is the distance from the light's respective sources to the point P and phi is the phase constant.  The superposition of these two waves is..

In a previous post I derived the equation for irradiance.  Using that definition..

If we were purely using the particle definition of light we would expect the irradiance would just be I1+I2.  The presence of the third term is an occurrence of the wave nature of light.  This term is deemed the interference term.  We now wish to examine the interference term more closely.  Taking the dot product and using a trigonometric identity..

For purely monochromatic fields, delta is time independent and the average of cosine simply becomes the cosine.  Real fields are not monochromatic and we must be careful when treating this time average.  We can find the irradiance of the two non-interference terms...

Where we have used the fact that the time average of a cosine squared function is 1/2.  This was shown in a previous post.  We can now write the interference term in terms of the two irradiances.

When light comes from two different light sources, the interference term is almost always zero.  This is because no light waves are 100% monochromatic and the time average between these two waves is equal to zero.  The way to represent this is to have phase functions instead of phase constants.  These functions are time dependent.

Beams that follow this are deemed mutually incoherent.    So basically, light beams from different light sources do not interfere with each other.
When the beams originate from the same source and are in phase, they are said to be mutually coherent and the irradiance interference term changes.  Namely, the phi's go to zero.  We will still write delta as the argument however.  Remembering that the cosine function oscillates between -1 and 1, we can get the following relations..

So the irradiance never goes completely to zero unless the two irradiances are equal to one another.  The general form of the irradiance of two beams of equal irradiance is...

Standing Waves, Interference and Group/Phase Velocities

Standing Waves:
When an electromagnetic wave comes into contact with a surface it is reflected.  This phenomenon is analogous to a mechanical wave created in a rope or a sound wave.  The reflected wave travels in the opposite direction with a phase difference.  We can therefore write both waves as..

Notice that the waves are indeed traveling in the opposite direction due to the plus and minus signs in their respective arguments.  Also notice both amplitudes of each wave are the same.  This is because we are modeling the standing wave to have equal amplitudes in both incident and reflective waves.  This means that no energy is absorbed in the reflection process or change in frequency.  If we super impose these two waves, we get... (Using some trigonometry.)

This expression represents the equation for a standing wave where the amplitude of the reflected wave is the same as the incident wave.  It was mentioned earlier that the wave undergoes a phase shift when reflecting off the surface.  It can be shown with Maxwell's Equations that this reflection phase shift is equal to Pi.  Therefore the above equation becomes...

One can interpret this expression as having a spatial dependent amplitude.  Meaning that the amplitude is different at each spot in space.  If we solve this amplitude for when it equals to zero, we can find the spots where the wave always has zero amplitude.  These points are called nodes.

There are also times where the wave is everywhere zero. These waves occur at the times the cosine term is equal to 0.

Similarly we can find the points where the wave is at a maximum and minimum.

If we have two mirrors and have an electromagnetic wave reflecting between them,  In lasers this occurs frequently.  We require the electric field to be equal to zero at each mirror, therefore the space between the mirrors can only hold a certain amount of wave lengths. The distance between the mirrors in terms of the amount of wavelengths between the mirrors is..

Where we have used half the wavelength because the electric field can be zero at a full wave length and a half wavelength.  Solving for wavelength we can find the frequencies of the standing wave modes.

These relations for frequency and wavelengths are strictly for plane mirrors.

Beats:
We now wish to superimpose two waves with the same amplitude, but different frequency.

Where w_p and k_p are the averages of the frequency and proportion constant respectively.  These are much higher than k_g and w_g which occur in the other cosine function.  Therefore one wave is a high frequency wave while the other is a low frequency wave.  The low frequency waves maps out the envelope of their superposition while the high frequency wave traverses in this envelope.  The envelope creates "beats" in the wave which can be used to send information.  The beat frequency is the difference between the two frequency of the two superimposed waves.

Phase and Group Velocity:
The general expression for velocity of a wave is...

The phase velocity is the velocity of the fast frequency wave inside the envelope.  And the group velocity is the velocity of the envelope itself.  Which are..

Where we have used the approximation that w1 is approximately equal to w2 which is approximately equal to w in a small neighborhood.  Same logic for k.  Plugging the phase velocity into the group velocity...

When the velocity does not depend on wavelength such as in a non-dispersive medium.  This would mean the phase and group velocities are zero.  This occurs in vacuum.  In a dispersive medium, v_p=c/n, where n is the refractive index.  The variable n is a function of lambda, meaning a function of k. n(k).